本サイトの姉妹サイト、「妖精⊸ロケット」では、WebGLを使ってウェブサイトを作るという実験を行っています:
これは「季節の歯車」です:
「季節の歯車」って、いったいぜんたい、何なのかって?
季節が毎年毎年一周してるのは、みなさんもご存知でしょう。ちかごろは、もう桜も散ってしまいましたもんね。
ところで。
なんで季節がきっちり正確に毎年一周しているのか、不思議じゃありません?
実はですね、…ここだけの秘密ですよ。
「季節」を動かす歯車、「季節の歯車」が毎年なんとなく一周しているから、季節は毎年一回だけ巡るのです。
じゃあ、その歯車が回るのはなんでなのかって?
それは、春香、夏美、秋葉、冬音の4人の精霊たちが、いつもは仲良く、時にはケンカしながら、「せかいの裏」でくるくる回しているからです。これも秘密ね。
春の次に夏がやってくるのは、春香と夏美が仲良くやってくれたから。
夏の最中に突然秋みたいな日がやってきたり、季節外れの台風がやってきたりするのは、…きっと、夏美と秋葉がたぶんちょっとした事でケンカしたんでしょうね。
でも大丈夫。ケンカしたら、仲直り。いつもそうやって、季節は巡ってきたのですから。
季節の歯車
…という創作神話(?)を元に、この季節を決める歯車である「季節の歯車」と、その結果生まれる「季節の巡り」をWeb上で表現してみようとしたのが、このWebサイトです。
もう少し常識的に言うと、左上の「歯車」の円周上に、それぞれの季節ごとの写真や絵、文章が並んでいます(これを「モーメント(瞬間)」と呼びます):

ここみたいな、いわゆる「ブログ」と違うのは、時系列で並べているわけではないことです。例えば、同じ「10月1日」の「モーメント」は、10年前のものでも今年の物でも、同じ角度のラインの上に並んで表示されます。
さらに、どの「モーメント」が表示されるかは、毎回ランダム(ガチャ)です。10年前の「モーメント」が表示されて今年の「モーメント」が表示されない事もあるし、逆もある。角度は同じでも、歯車からの距離は更新するたびに変わります。この点でも、2018年のページをクリックすれば必ず2018年のページが表示される「ふつうのブログ」とは異なります。
WebGLでウェブサイト作ろうぜ
えー。「季節の歯車」の紹介はこれぐらいで置いておいて。この季節の歯車を表現するための技術について、がこの記事のテーマです。
このウェブサイトは基本的に全部WebGLと、素のECMA Script 6で書かれています。くるくると回る「歯車」も「モーメント」も、全部WebGLで描いていて、HTMLの<img>タグとかは使ってない、と言うことです。もちろん、WebGLはCanvasの中身をOpenGLで描ける、という技術ですので、他のHTMLの技術と、簡単に組み合わせることもできます。「季節の歯車」では、「モーメント」の上にマウスが乗ると、タイトルが表示されるようになっています。この表示に使われているのは、いつもの<div>要素です:

3Dオブジェクトの当たり判定
さて、これで困るのは、マウスの判定です。つまり、マウスがどの「モーメント」の上にあるのか(あるいは無いのか)のチェック関数、です。
HTMLのmouseoverイベントは使えません。「モーメント」は全て、HTMLの要素ではなく、1つのcanvas要素の上にOpenGLで描かれている「絵」に過ぎないからです。
canvas要素のmousemoveイベントを使えば、canvas上でのマウスの座標を得ることはできますが、この座標もそのままでは使えません。というのも、「モーメント」も左上の歯車と同様、「遠近法」が掛かっている立派な「3Dオブジェクト」だからです。
まぁ、わざわざ「遠近法が掛かっています」と上でわざわざ書いたように、事実上ほとんど掛かっていないので、2Dだと思って当たり判定を書いてもほとんど困ることはない(見ている人が気づくことはない)かもしれません。
でも、せっかくだから「正確」に判定してみたい。趣味のプロジェクトですしね。
さて、こういう「3Dのオブジェクトとマウスの当たり判定」じたいは、ゲームではよくることです。3D空間内のアイテムをマウスでクリックして取得したり。このためのテクニックは「Object picking」と呼ばれているそうで、よくある実装は、「当たり判定」のための専用の画面を作ってしまうというものです:

まず、オブジェクトごとに相異なる色で塗った「別の画面」を作ります。この画面は、ユーザーには見せません。ただし、あたり判定をする時は、この隠れた画面からマウスの位置にあるピクセルを読んで、「何色」になっているかを調べます。この色が何色かで当たり判定をする、と。例えば上の例だったら、一番明るい灰色だったら右のチェス、真っ黒だったら背景(何とも当たっていない)、といった感じです。
うーむ。たしかに、チェスの駒とか、人間、動物みたいな、複雑な形のオブジェクトがたくさんある中から当たり判定をしたいならわかります。むしろ、この方法を取らざるを得ないでしょう。
でも、ただの「パースのついた丸」のためにこれをやるのは何だか大げさというか、資源の無駄遣いな気がします。単純に2回絵を描かないといけないですし。「相異なる色」を用意したり、半透明になったりしないように配慮した別の描画プログラムをもう一つ用意しないといけないのも大変です。
もっといえば、この「別の画面を用意して、あたり判定を行いたいオブジェクトごとに色を塗る」という力技で当たり判定ができるのは「当たり前」すぎるように感じられます。ちょっと面白くない。
そこで今回は、それとは別のアプローチを考えてみましょう。
「遠近法」のおさらい
その前に、まずコンピューター3Dにおけるいわゆる「遠近法」をおさらいします。
「いわゆる」とつけたのは、「遠近法」と言えそうなものは、このコンピューターの世界の中だけでもたくさんあるからです。わたしの考えでは、ラスタースクロールも遠近法ですし、ゼビウスのゲームシステムも、「空気遠近法」と同じくらいには、りっぱな遠近法だと思います。
とはいえ、「季節の歯車」では、コンピュータ3Dの世界で「遠近法」という言葉で指すものの中では最もおなじみであろう、「透視法射影」を使っています。
これはどんなものだったのか、と言えば、表示したいモデルの頂点の三次元空間上の座標、x y z、そして最後に1を立てたベクトル(x y z 1)に、モデルごとの変換行列Mを掛けて、出来たベクトルをさらに最後の要素( wと呼ばれる事が多い)で割り、出来た(x’/w’ y’/w’)が画面上での最終的な座標となるのでした。
わかりにくいので、ちょっとベクトルがどのように変形されていって最後のxy座標になるまでを図にしてみました:
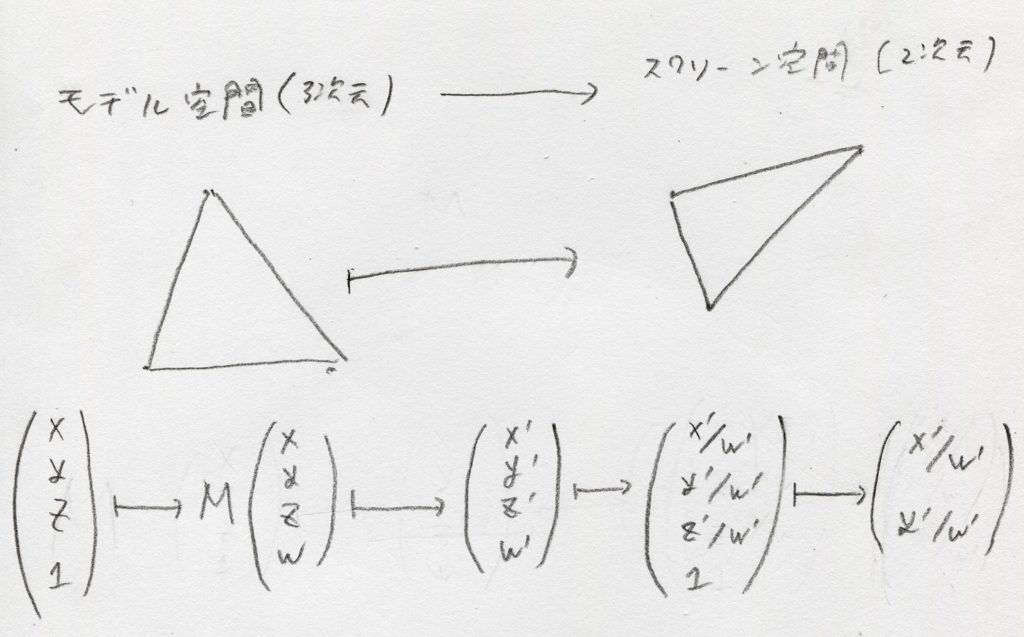
それぞれの操作を、数学で写像で移される時元の対応を表す、↦のマークを流用してその処理の流れを表現してみました。えっ、数学の世界でそんなに繋げるような記法は普通しない?まぁまぁ。うまい表記が思いつかなかったので、おもいついた人は教えてくださいな。
行列Mについて少しだけ話をさせてください。このMをうまく作ることで、モデルの平行移動や、回転、拡大縮小を表現できるだけでなく、最後にw’で割るという、行列のかけ算だけでは表現できない非線形な操作と組み合わせることで、遠いものほど小さくなる「遠近法(パース)」が再現できます。上手く作る、といっても、glMatrixなどのいわゆる3D向け行列ライブラリを使えばそんな難しくないです。とりあえず、この話はまた別の機会にいたしましょう。
さて、元々やりたかった事は何かというと、パースの掛かった「丸」とマウスのあたり判定でした。
ふむ。残念ですねぇ。何がって?パースの掛かった「三角形」とのあたり判定だったらすごく楽だったからです。あたり判定の対象が三角形であれば、上の操作で作ったスクリーン上の3つのXY座標で囲まれた三角形の中にマウスの座標があるかどうかを判定するだけで済みます。とはいえ実はその判定はそこまで簡単でもないんですが、やること自体は直感的です。

一方、パースのかかった丸となると、どうすればいいのやら。斜めになってるとぐにゃぐにゃした形になっていて、何をどうすれば内側になるのか判定できるのか、よくわかりません。
スクリーン空間からモデル空間へ
遠近法をつけた丸はぐにゃぐにゃしてて、なんかよくわかりません。となると、遠近法を付ける「前」の丸とマウスの当たり判定を行う作戦を取らざるを得なさそうです。遠近法を付ける前なら、単に「円の中心とマウスの座標の間の距離が円の半径以下か」判定すれば良いだけですから、三角形の内側にあるかどうか判定するよりも更にラクです。まぁ、点と点の距離を調べるのも、実は言うほど簡単じゃあないんですが…。
閑話休題。そうなると、問題は「マウスのポインタは、元のモデル空間では一体どこに存在するのか?」になります。さっきの図はモデル空間からスクリーン空間の話でしたが、今度はその逆、スクリーン空間からモデル空間への話を考えねばなりません。二次元から三次元上の位置を推定しないといけないので、ややこしそうです。
一つずつじっくり追い込んでいきましょう。まず、モデル空間上にあるマウスの点を(xm ym zm)、液晶画面上のマウスの座標を(xs ys zs)とします。マウスの座標にZ軸なんか存在しないのですが、あとで計算するときに便宜上必要になりますので「未知だが、存在する、何かしらの数」として導入します。
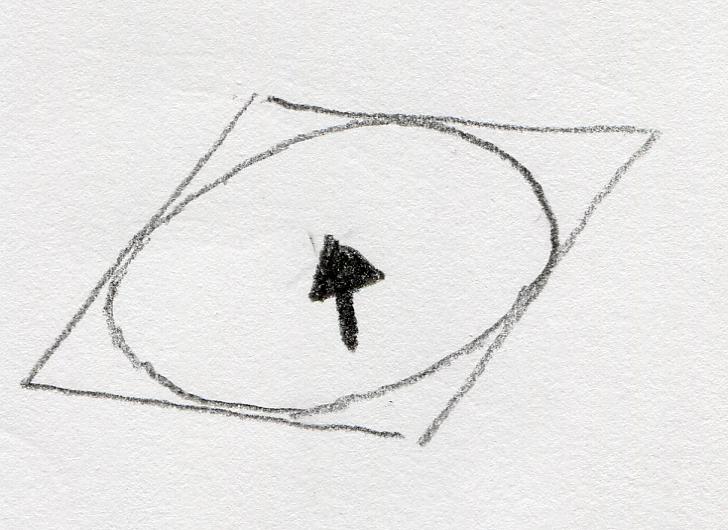
さて、目からマウスポインタを結ぶ線は液晶モニタの平面を貫通し、最終的に液晶モニタの後ろにある(笑)1モデルへとぶつかります。図にするとこんな感じです:

これらの(xm ym zm)と(xs ys zs)の関係を、書いてみます:
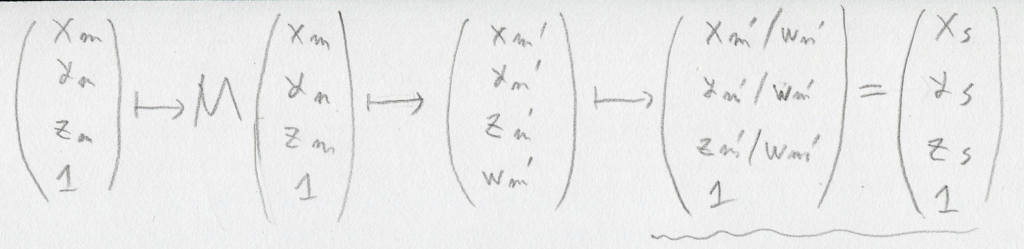
この図自体は最初に描いたものとほぼ同じです。
なかなかややこしいので、wsという(未知の)変数を新たに導入した上で(といってもw’mのエイリアス)、まず波線を引いた部分を変形します。
行列を掛けて出てきた、素性のよくわからんx’m, y’m, z’mを、すでに分かっているxsやysなどにできるだけ置き換えいって整理しようという作戦です:
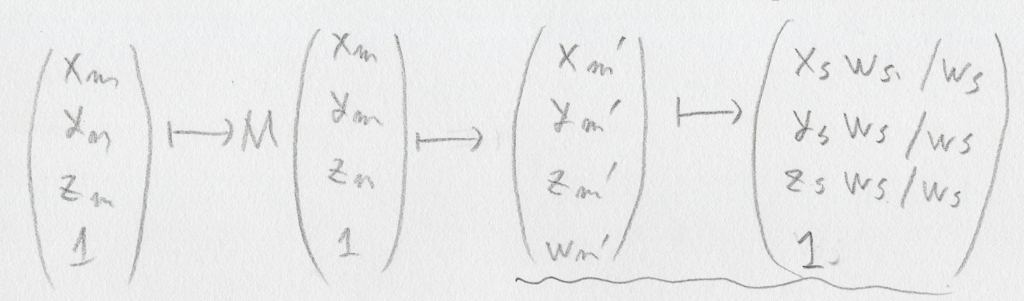
さらに波線のwで割ってる部分も、xs や ws を使って割ってない所まで戻します。
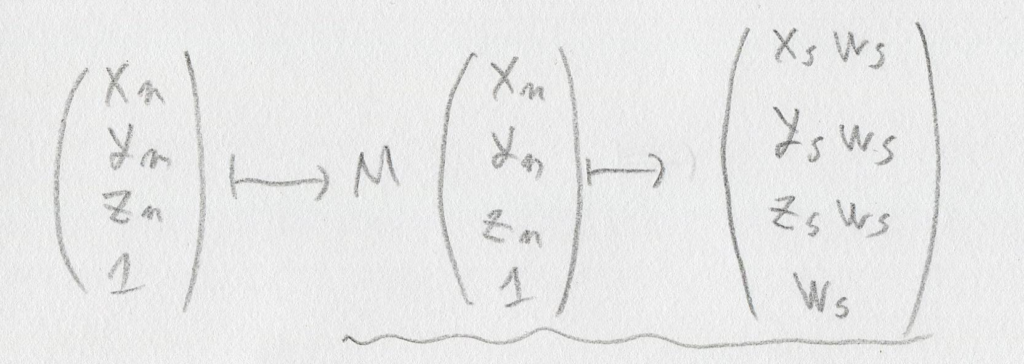
すると、「モデル空間上の座標に変換行列Mを掛け算して移すと、スクリーン空間上の値を使ったよくわからんベクトルができる」、という図になりました(少なくともわたしはそういう意味でこの図を書いてます)。波線の引いた部分は「矢印の左側でベクトルに行列をかけると矢印の右側のベクトルになる」、という意味で使ってますので、おなじみの等号に書き直します:
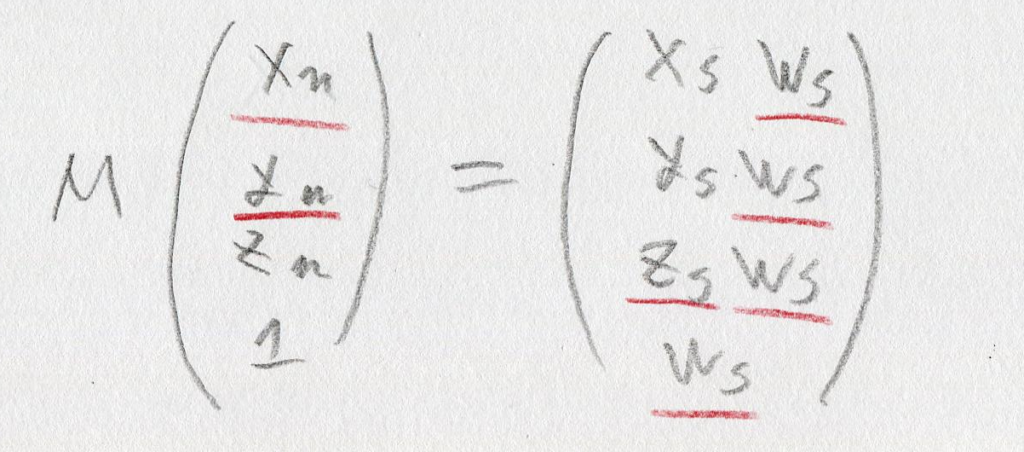
未知変数の部分に赤線を引いてみました。xm ym zs wsの4つが未知で、Mは4×4の行列ですから、この行列とベクトルの式は実際には4本の連立方程式です。未知数が4つで、式が4本。原理的には解けます。やったね。zmは未知じゃないのかって?あー、言い忘れてました。今回の丸は、モデル空間上ではXY平面上にあることにしましょう。なので、zmはzm=0の定数です。
さて、この式は前述した通り解けるので、xm ym zs wsを求めたら、zsとwsは単に便宜上入れた要らない変数なので捨ててしまいましょう。モデル空間上のマウスの座標である、xmとymを使えば、無事円との当たり判定ができます。
はいおしまい、QED。
…と言いたい所だが、この行列は実際一体どう解いたらいいのか?右にも、左にも未知変数があります。逆行列を一発キメたら終わり、みたいな、そういう生ぬるい式ではなさそうなのは確かです。かといって、プログラムに組み込んで自動で解かなければならない以上、「頑張って手動で連立方程式を変形して解く」みたいな高校生的解法は使えません。捻りが必要です。
頑張って式を変形するぞい
まず確認です。行列とベクトルの掛け算とは、行列の各行ベクトルを、もう片方のベクトルのそれぞれの値で重み付けをして足し合わせることだと見なすことができます。
左辺
まず左辺をこれを使って変形します。Mを、M1からM4までの4つの縦ベクトルが横に並んだものだとみなすことにしました:
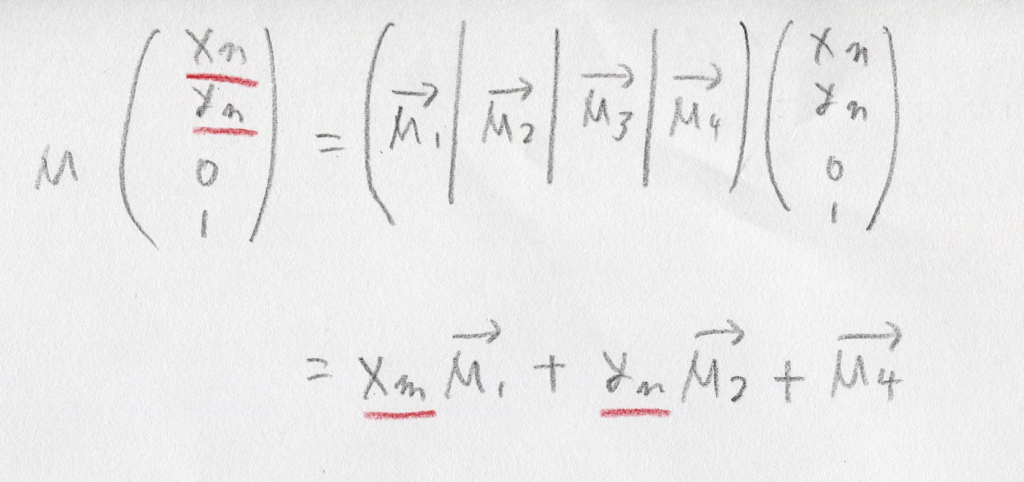
右辺
次は右辺です。右辺は、まずwとx y zが掛かっていて複雑なので、wをくくりだします。

赤線を引いた未知変数がだいぶ減って気楽な感じになりましたが、まだベクトルの中と外に未知変数が入っていて扱い方がわかりません。さらにこれをこんな感じで2つのベクトルの和に変形します。
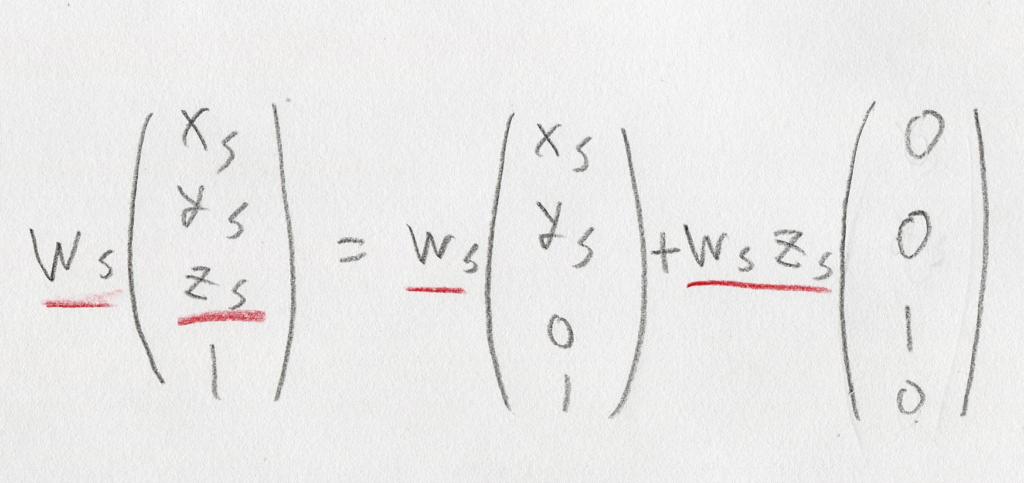
するとどうでしょう。右辺も左辺も、「「未知のスカラ量 x 既知のベクトル」の和」に変形できました。
なんとなく、これなら扱えそうな気がしてきません?
最後の一捻り
さっき変形した右辺と左辺の式を使って、再度等式を書いてみます:
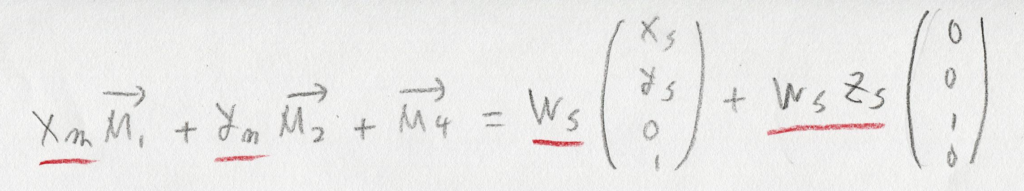
するとただの和なので、簡単に未知変数を左辺だけに集約することができます:
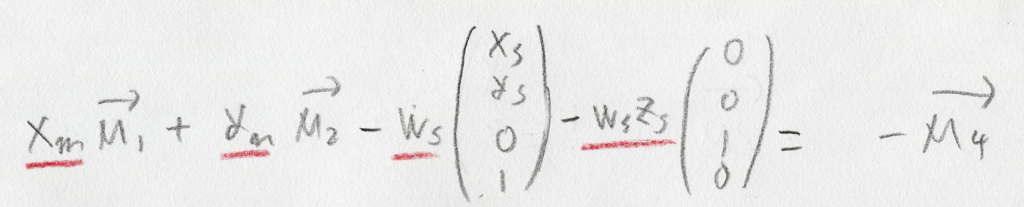
で、ここで最後の一捻りです。
さっきの
行列とベクトルの掛け算とは、行列の各行ベクトルを、もう片方のクトルのそれぞれの値で重み付けをして足し合わせることだと見なすことができます。
というのを、今度は逆回しにします。つまり、こんな感じでもう一度「行列とベクトルの積」に書き戻します:
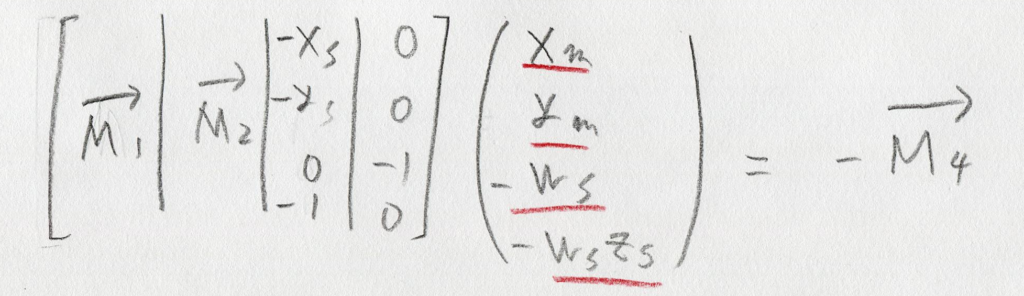
ここまでくれば、もう簡単。赤線が引いてある未知変数が詰まってるベクトルの値は、逆行列を掛ければ一発で求められます。
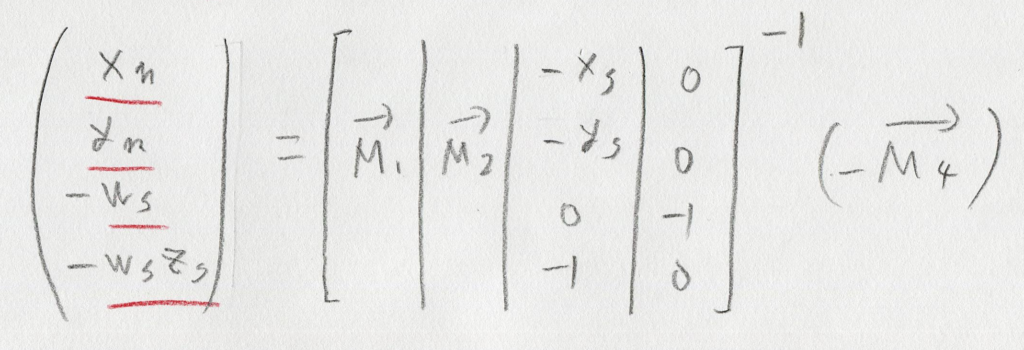
長かったですけど、纏めてみると結構綺麗な解法のような気がする。…どうかな。
JavaScriptで最小のデモ作った
「季節の歯車」だとここで実装してるんですが、流石に他のコードも多くてわかりにくいだろうという事で、この当たり判定の部分だけ切り出したサンプルを作ってみました:
github.com/ledyba/__sample__3d-picking-without-shaders
パースのついた円とマウスの当たり判定をする
実際に動いてるデモのページはこちら。
- でも、最初にプレステのゲームを遊んだときは、そんな感じがしませんでした? [↩]