今日の朝、ストップウォッチと電線を使って月の天球上での直径を計測したところ、約0.6度と出ました。

…さて、この値はどこまで正しいのか？

それを確かめる一つの方法は、「正解」を直接ググることです。が、それはあんまりにも面白くない。

そこからは少し離れた情報との整合性を、確かめてみようではありませんか。

それは、月の距離と直径です。それぞれ約38万km、3500km。小学校教育と中学受験のせいかおかげか、脳の中に、刷り込まれ、今でも、亡霊のようにこびりつき、こだまする、この「「「事実」」」と、どれほど一致するのかの概算をします。

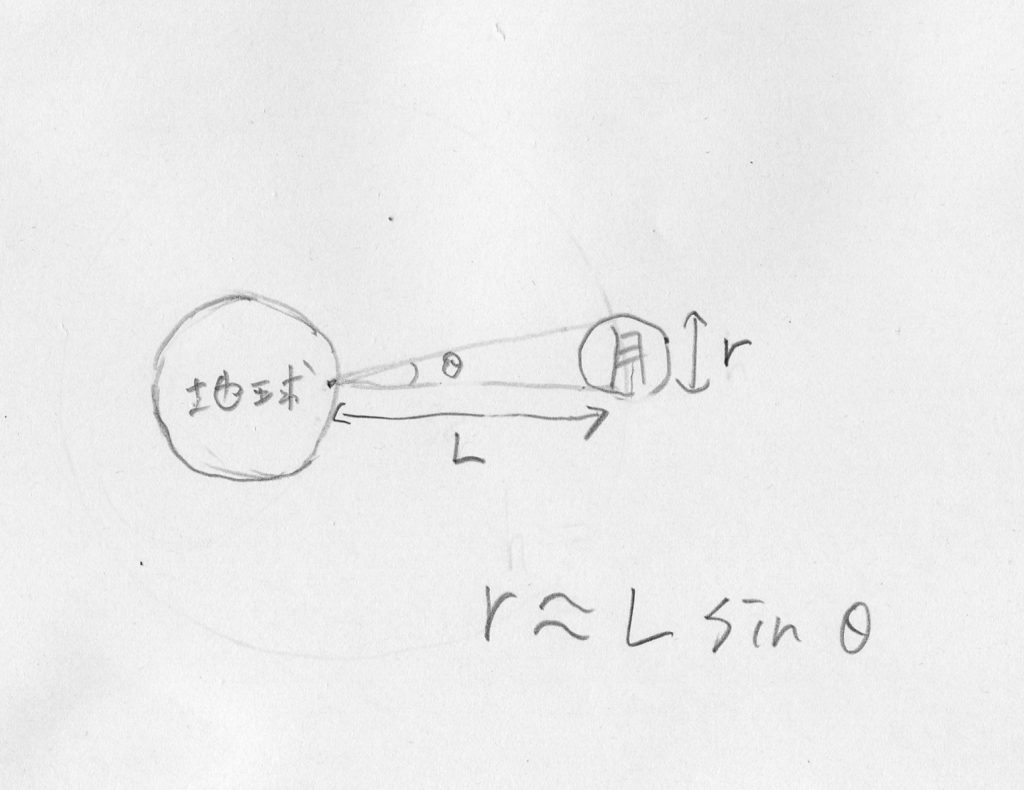
三角関数で計算する

月までの距離と、月の天球上での直径（角度）が分かれば、三角関数を使って月の直径を計算することができます：

>>> 38*10000 * math.sin(0.6*math.pi/180.0)
3979.277964173401

実際に数値をいれて計算すると、約4000kmと出ました。文部科学省の提唱する「約3500km」と比べるとちょっと大きいですが、倍か半分ぐらいまでの差は出るだろうな思っていたので、それに比べたらだいぶ近い値が出ています。正直、ちょっと驚いています。

テイラー展開でも計算する

さて、仮に文明がいますぐ何らかの理由で崩壊し、コンピュータの提供する便利なsin関数が使えなくなっても、0度近辺でならsin(x)はxで近似できる（テイラー展開）ことを知っていれば筆算で計算することができます：

>>> 38*10000 * (0.6*3.14159265358979/180.0)
3979.3506945470676 #ほんとに筆算しようと思ったが、めんどくさくなってやめた

上の数値と見比べると、38万kmも先のことを計算したのに、100mも差は出ません。実を言うと大学受験の数学や物理の問題か、大学の数学や物理の試験問題でしかテイラー展開なんか使った事がなかったもので、ここまで差が出ないのかと、またもや驚いています。

しかし、でも、ちょっと大きい。

とはいえ、この結果は、教科書に書いてあった「約3500km」に比べるとちょっと大きいのも事実。この計算につかった「約0.6度」は、地平線近くで測ったものです。地平線の近くにある月は、なんとなく、空の上にある月より大きい気がしませんか。それは人間の錯覚なのか、それとも何らかの理由（大気の屈折とか？）で本当に見かけ上大きくなっているのか。

空の上の方の月でも測定して、もう一度同じように計算してみたいです。

しかし、天気予報によれば、これから先しばらく曇りとのこと。

うーん…次の半月か満月の晴れた夜までに、使えそうな電線を見つけておくことにするか。