月を眺めていると、その動きはかなり速いことに気が付きます。

昔のアニメのお歌で「ぼくもわざと立ち止まれば　月も立ち止まる」なんてことばがありましたが、実際に立ち止まってみると、そんなことはありません。動いてるのが目視で分かるくらいの速度で、ゆっくりですが、「歩いて」います（もちろん、だからこのお歌はだめ、なんてことはないですよ）。

さて、このことを使って月の大きさを測ってみました。

方法

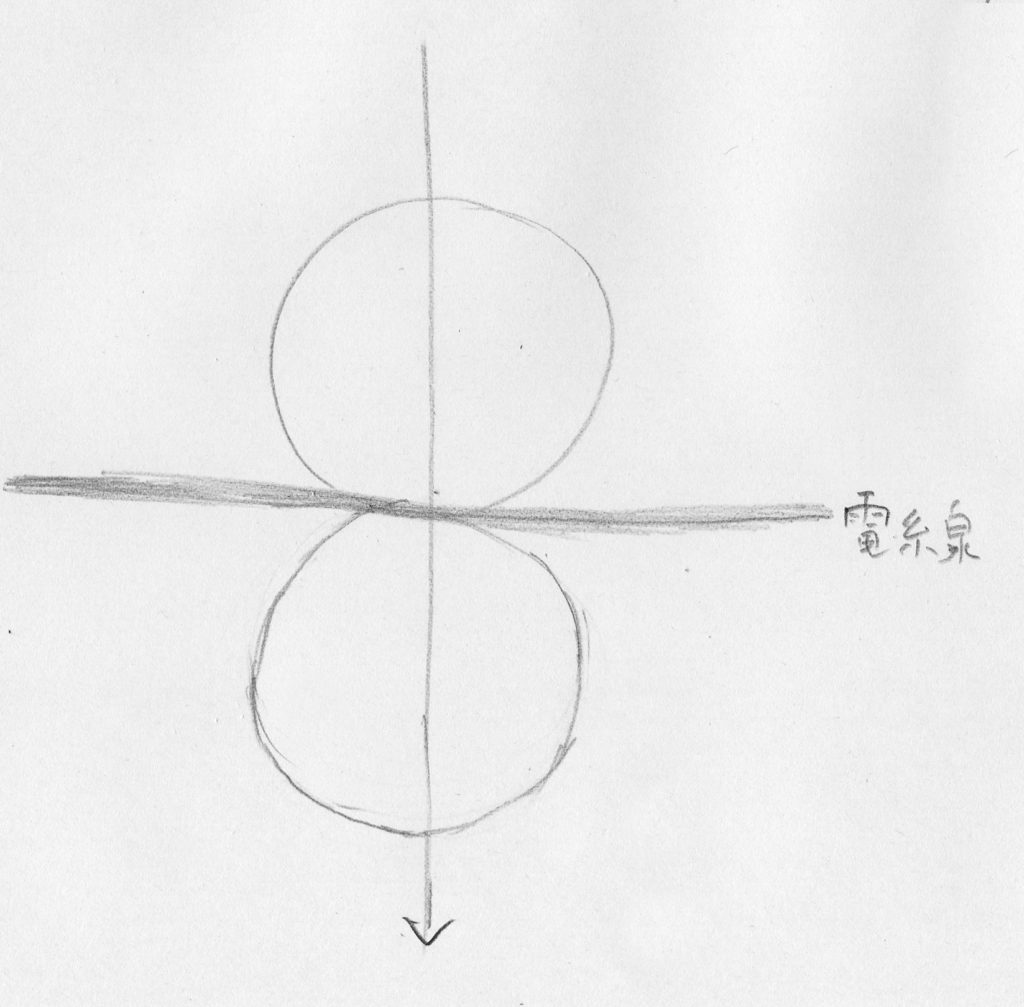
月の進行方向と、できるだけ直交する電線を選びます。適当な電線に月が触れるのを眺めたら、ストップウォッチで測定を開始します。そして、月が電線から離れた瞬間に測定終了。その時間を記録して「月の大きさ」とします。「時間」ですが、「大きさ」です。

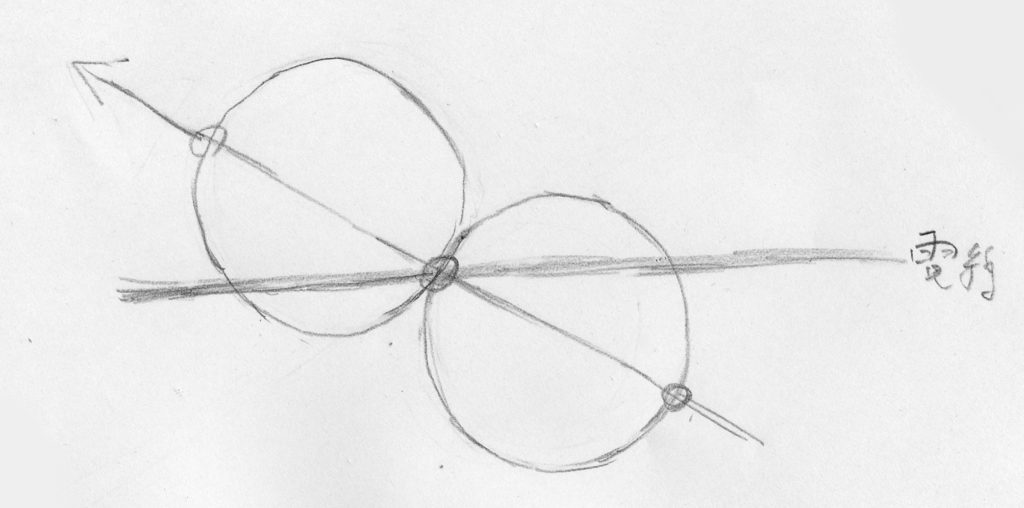
電線と月の移動する向き（進行方向と呼ぶことにします）は一般にはさまざまな角度をなします。電線と月の進行方向が直交することも、ほぼ同じ方向になることも、ナナメになることも、あるでしょう。「月が電線を横切る時間」を、「月のどこかが電線に触れてから月が完全に電柱から離れるまで」と定義すると、この電線と月の進行方向がなす角度によって、時間が変わってしまいます（すんごい極端な例を考えるとはっきりします）。

月と月の進行方向の直線がまじわる２点を基準にして、この２点が電線と触れる時間と定義して測れば、電線と進行方向の角度の影響を無視できそうな気はするのですが…

まぁ、練習が必要そうなので、今日は「電線と進行方向ができるだけ直交する」一番単純な場合を使って測定します。

結果

4月21日　朝

今日は満月から１日ほど経ったころ。測定結果は次の通りです：

• 2分16秒
• 2分23秒

今日は水平線近くが白くて区別がつかなくなってきたので、３度目は断念しました。

約2分20秒とすると、月は29.5日で公転し、地球は１日で自転するので（意図的に細かいところをあえてガン無視している）、このことを使って計算します。

% python
Python 2.7.16 (default, Mar  6 2019, 18:14:51) 
[GCC 5.4.0 20160609] on linux2
Type "help", "copyright", "credits" or "license" for more information.
>>> moon = 360/29.5
>>> earth = 360.0/1.0
>>> (moon+earth) * 140 / (24*3600.0)
0.6031073446327683
>>> 

天球上の角度はだいたい0.6度？ってことでいいのかな？

今後

理科年表にひょっとすると月の大きさが書いてある気がしてならないのですが、見ないで独自研究をすすめてこうかな。ちょっと悩んでます。

「月の満ち欠けみたいに　幸せも 大きくなったり 小さくなったりする」なんて歌詞もあるとおり、月には満ち欠けもあるわけですが、今回の方法を使って月齢を（定量的に）測れたらちょっと面白い気がしています。この場合、月の進行方向と電線の角度にはもっと気をつけないといけないでしょうなぁ。

あとは…そうですねぇ、地平線の近くにあると月は大きく見えるわけですが、これが本当なのかどうか、実測してみたいかも。

太陽

太陽も測ってみたいが、どうすればよいのか…陰を使えばいいのだろうか。

ストップウォッチやめたい

ここでテクノロジーに頼ってるのすこし違和感があるので、ストップウォッチもやめたいんですが、時間を測定するいい道具ないかな。月が電線を横切る時間と、一日の長さ（「日の出から次の日の日の出までの間」としましょう）を同時に測定できる道具…なんだろ。