こんな感じの逆説（パラドックス）です．

あるバードウォッチャーは「すべてのレイヴン（からす）は黒い」という仮説を証明しようと思っている．

この説を証明するには，レイヴンを探し出してその色を調べればよい．

黒いレイヴンがみつかれば，仮説の確認例となる．

逆に黒くないレイヴンが見つかれば，この仮説を否定することになる．

赤いレイヴンが一羽でも見つかれば，もうレイヴンを探す必要はない．仮説は間違いなのだから．

この仮説は「すべての黒くないものはレイヴンでない」と言い換えることも出来る．

（理論学からすれば，これは元の仮説と同値である．「対偶」という．）

この仮説はずっと確かめやすい．黒くないものを見て，レイヴンでないと確認すれば，それは仮説の確認例になる．

ここにピンク色のゲームパッドがある．これはさっきにも述べたとおり，「すべてのレイヴンは黒い」の確認例になる．

（ほんの少しだが）

このゲームパッドは同時に「すべてのレイヴンは白い」の確認例にもなる．

（対偶は「すべての白くないものはレイヴンでない」から．白くもないし，レイヴンでもない．）

ひとつの観測結果が相反する二つの仮説の確認例になることはない．

そんな新奇なことを認めたら，なんでも「証明」できてしまう．

ゲームパッドがすべてのレイヴンが黒いことと，白いことの確認例になる．

ゆえに

「白は黒である」

証明おわり．

（「パラドックス大全」よりほぼ引用．すこし違いますけどねｗ）

・・・斑鳩はどうなるんだって話ですねｗ

とまあそれはさておき．

本当に対偶は元の仮説と一緒なのか？

これは重要ポイントの一つですよね．

「パラドックス大全」では集合論なのにベン図もつかわず文章だけでだらだら書いてるんですが，分かりづらくってしょうがない．

いかにベン図を示すので確認してください．

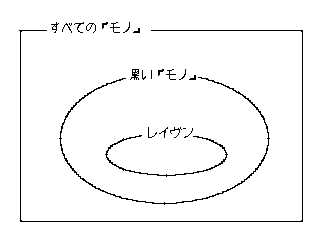
「すべてのレイヴンは黒い」を満たす場合です

「すべての黒くないものはレイヴンでない」も満たしてます．

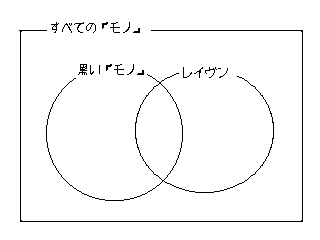
黒くないレイヴンも居る場合です．

「すべてのレイヴンは黒い」を満たしていません．

「すべての黒くないものはレイヴンでない」も満たしてません．

積集合がない場合も考えられますが・・・まあ書いて見てください．同じです．

というわけで，対偶は同じ．

「すべてのレイヴンは黒い」はレイヴンは最低一匹居るのを前提としているのに，対偶はそうでない，なんて話題もありましたけど・・・．

まあ，そうですけど，一匹レイヴンを見ればいいだけの話なので，実質同じですよね．

で，答えは？

色々話題を出す割には明確な答えが書いてない気がする．

「対偶で証明するのは確かに間違ってないけど，アホらしい」くらいの事しか読み取れないんですけど．

しゃーないので自分なりに結論．ちなみに，書いてあること殆ど参考にしてません（意味無いじゃん）．

この逆説でおかしいのはここ．

ひとつの観測結果が相反する二つの仮説の確認例になることはない．

いえ，なるんですよ．

以下のベン図を見てください．

「ピンクのゲームパッド」は斜線の部分に含まれて居ます．

仮に斜線部分をすべて調べたとすると・・・その観測結果はどういう結論をもたらすでしょうか？

「レイヴンは黒いか白い」という結論になりますよね．レイヴンは今のところ一匹も見つかってないんだから，黒の集合か，白の集合か，もしくは両方のどれかに含まれるわけです．

ですから，白くも黒くもない「ピンクのゲームパッド」は「すべてのレイヴンは白か，もしくは黒」の確認例になるんです．

また，「すべてのレイヴンは白か，もしくは黒」という仮説は，「すべてのレイヴンは黒」と「すべてのレイヴンは白」をそれぞれすこしずつ支持する仮説ですよね．

ですから，「黒は白である」は間違いである，という結論になります．

ああ，良かった．これで今日も斑鳩三昧ですよ（笑